Penrose II
tl;dr I finally figured out how to algorithmically align the rhombuses to form a Penrose tiling! The main idea is the classic breadth-first search.
The source code is here.
The animation you see above can be found on the visualization branch.
Background
This is a follow-up on my previous post Penrose, where I used de Bruijn’s pentagrid method to generate Penrose tilings. However, I only successfully placed the rhombuses at the intersection of the grid lines. But these were only the initial locations of the rhombuses. We still need to align them. I didn’t figure out a way to automatically do this. So I ended up making it a “game”, where people can use the mouse to drag rhombuses and manually align them. You can try it here. However, after ten months of pondering, there is now an “Align Rhombuses” button, which can do the job for you!
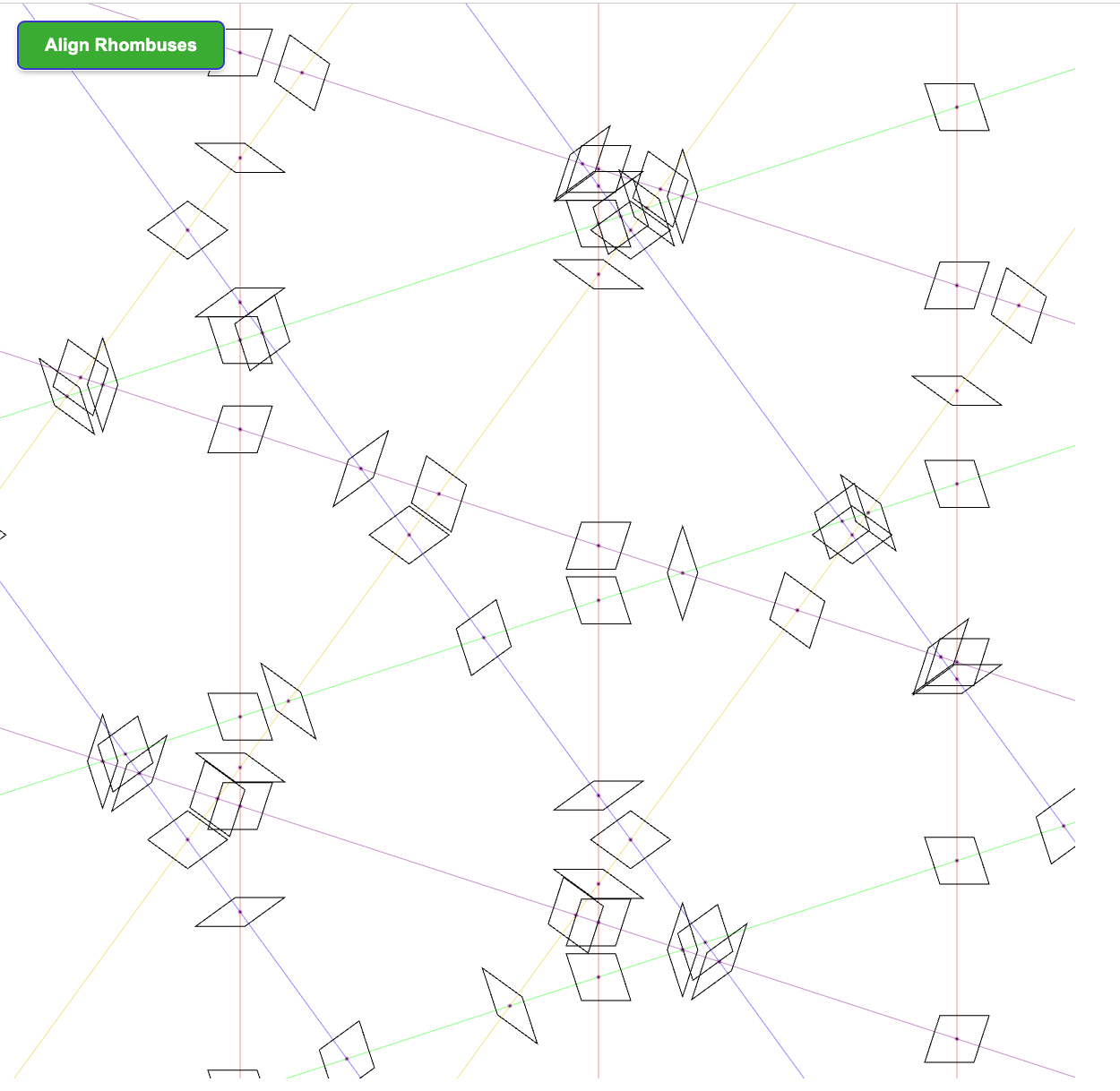
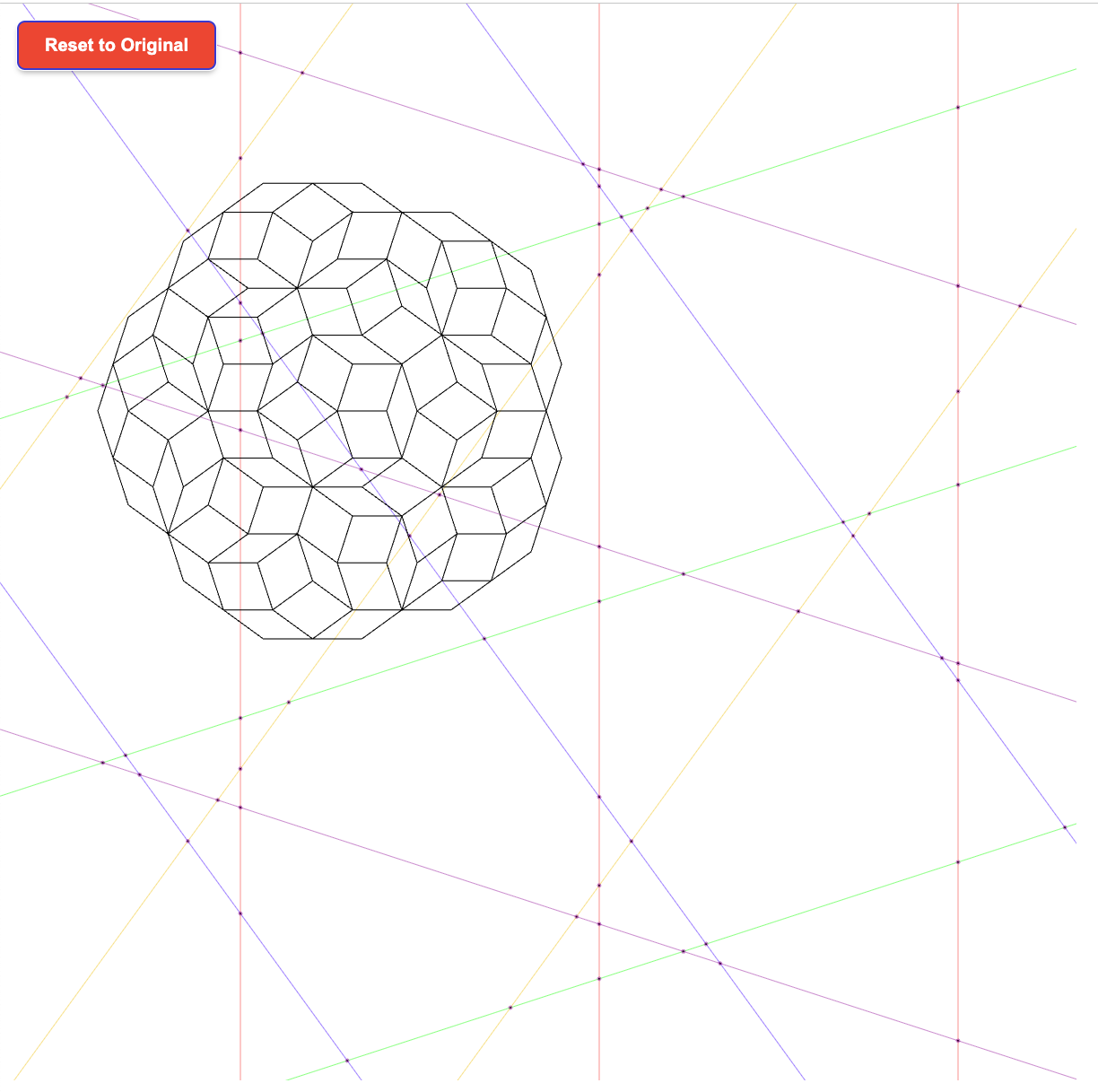
A special thank you to Professor Kaplan who replied to my emails with the idea of using breadth-first search and debugging suggestions. The moment I connected all the dots was when reading this math StackExchange post. Knowing that someone has done this successfully before greatly boosted morale.
Algorithm
Because we are going to use the breadth-first algorithm, the first step is to construct a graph.
The vertices of the graph are rhombuses.
There is an edge between the two vertices if and only if the rhombuses are “next to each other”.
Specifically, two rhombuses are next to each other if they are on the same grid line
and there are no other rhombuses between them on that grid line.
Now with this graph, we start with any initial rhombus and find all its four (there are always four) neighbors.
We move the neighbors so that their “closest” edges are aligned.
Closest here cannot always be measured by the Euclidean distance because the rhombuses might overlap.
The closest edges are defined once we create an edge between two rhombuses R_x and R_y.
Without loss of generality, we assume that R_x is to the “left” of R_y,
therefore, the “right” edge of R_x needs to be aligned with the “left” edge of R_y.
I couldn’t find a more rigorous mathematical way to describe this.
The idea is to use the grid lines of the intersection that each rhombus lies on to
determine their relative position.
I hope the intuition is clear here.
After this step, we iterate over newly aligned rhombuses in a first-in-first out order,
finding and moving their neighbors.
Implementation
I used Claude Code (CC) a lot. I even hit the daily usage quota because I only have a normal subscription account. However, I had to give VERY specific instructions. Giving the high level idea, such as “next to each other”, did not work. CC chose to use the distance between vertices, which is not always correct because sometimes the rhombuses overlap. Similarly, I had to explicitly state the definition of the “closest edges”. Unlike other tasks I’ve worked on with CC where it was able to figure out the solution given very high-level instructions, I needed to “micro-manage” it this time. This is probably because Penrose tiling is not a very frequent topic in its training data. And it hasn’t seen the exact code I wanted and couldn’t retrieve the solutions from memory. This is the commit where CC finally implemented everything exactly as I wanted. To be honest I didn’t review the code too carefully since the results looked correct. One day I will come back and read/study the code CC wrote to improve my JavaScript coding ability.